SODOKU UNA HERRAMIENTA EFICAZ PARA PRACTICAR LÓGICA MATEMÁTICA

Sudoku (en japonés 数独, sūdoku) es un juego matemático que se inventó a finales de la década de 1971, adquirió popularidad en Japón en la década de 1980 y se dio a conocer en el ámbito internacional en 2005 cuando numerosos periódicos empezaron a publicarlo en su sección de pasatiempos.
El objetivo del sudoku es rellenar una cuadrícula de 9 X 9 celdas (81 casillas) dividida en sub-cuadrículas de 3 X 3 (también llamadas "cajas" o "regiones") con las cifras del 1 al 9 partiendo de algunos números ya dispuestos en algunas de las celdas. Aunque se podría usar colores, letras, figuras, se conviene en usar números para mayor claridad, lo que importa, es que sean nueve elementos diferenciados, que no se deben repetir en una misma fila, columna o sub-cuadrícula.
Reglas y terminología
El sudoku se presenta normalmente como una tabla de 9 × 9, compuesta por sub-tablas de 3 × 3 denominadas "regiones" (también se le llaman "cajas" o "bloques").
Algunas celdas ya contienen números, conocidos como "números dados" (o a veces "pistas"). El objetivo es rellenar las celdas vacías, con un número en cada una de ellas, de tal forma que cada columna, fila y región contenga los números 1–9 solo una vez.
Además, cada número de la solución aparece solo una vez en cada una de las tres "direcciones", de ahí el "los números deben estar solos" que evoca el nombre del juego.
Métodos de resolución
La casilla marcada en verde de la región 3 × 3 de la esquina superior izquierda debe contener un 7.
La estrategia para resolver este rompecabezas se puede considerar como la combinación de tres procesos: rastreo, marcado y análisis.
Rastreo
En el ejemplo anterior, rastreando a lo largo y ancho los sietes localizados en cualquier lugar de la rejilla, el jugador puede eliminar todas las celdas vacías de la esquina superior izquierda que no pueden contener un 7. Esto deja sólo una celda posible (marcada en verde).
Marcado
El rastreo viene a interrumpirse cuando no pueden descubrirse nuevos números. En este punto es necesario centrarse en algún análisis lógico. La mayoría encuentra útil guiar este análisis mediante el marcado de números candidatos en las celdas vacías. Hay dos notaciones populares: subíndices y puntos.
En la notación de subíndice, los números candidatos se escriben en pequeño en las celdas. La desventaja es que los rompecabezas originales se publican en periódicos que habitualmente no dejan demasiado espacio para acomodar más que unos pocos dígitos. Si se usa esta notación, los resolutores crean, a menudo, una copia más grande del rompecabezas y emplean un lápiz afilado.
La segunda notación es un patrón de puntos con un punto en la esquina superior izquierda representando un 1 y un punto en la esquina inferior derecha representando un 9. Esta notación tiene como ventaja que puede usarse en el rompecabezas original. Se requiere destreza para el emplazamiento de los puntos, porque la existencia de puntos desplazados o marcas inadvertidas lleva, inevitablemente, a confusión y no son fáciles de borrar sin añadir más confusión.
Análisis
Hay dos aproximaciones principales:
- En eliminación, el progreso se realiza mediante la sucesiva eliminación de números candidatos para una o más celdas, hasta dejar solo una elección. Después de lograr cada respuesta, debe realizarse un nuevo rastreo (habitualmente comprobando el efecto del último número). Hay una serie de tácticas de eliminación. Una de las más comunes es el "borrado del candidato no coincidente". Las celdas con idéntica configuración de números candidatos se dice que coinciden si la cantidad de números candidatos en cada una es igual al número de celdas que los contienen. Esta aproximación puede ser desaprobada por puristas lógicos por demasiado ensayo y error pero puede llegar a soluciones claras y rápidamente.
- Idealmente, se necesita encontrar una combinación de técnicas que eviten alguno de los inconvenientes de los elementos de arriba. El recuento de regiones, filas y columnas puede resultar aburrido. Escribir números candidatos en celdas vacías puede consumir demasiado tiempo. La aproximación "y-si" puede ser confusa a menos que se sea bien organizado. La intención de la cuestión es encontrar una técnica que minimice el recuento y el marcado.
EJEMPLOS:


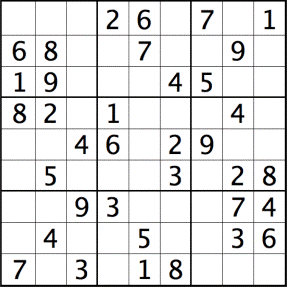

Comentarios
Publicar un comentario